
 |
Eager Space | Videos | All Video Text | Support | Community | About |
|---|



The current starship is 9 meters in diameter. SpaceX has plans to stretch both starship and super heavy to make them slightly taller to carry more fuel, but Musk has talked about versions that would be bigger in diameter.
Starship is already the biggest rocket ever and handling it poses some unique challenges. Why would you want to go bigger?
It turns out that there's a pretty good reason to consider going bigger, and it's all about propellant tanks, because rockets are mostly tanks with engines stuck on the bottom.

Real tanks have domes at the top and bottom to better deal with pressure, but it's simpler to just consider the tanks to be cylinders. Doing the same calculations with domes is left as an exercise for the viewer.
What we want to do is figure out how efficient a tank is - how much material it takes to create a tank that can store a given volume of propellant
We'll be looking at cylinders based on their height and their radius, which is half of their diameter
The volume is equal to the area of the end of the cylinder, which is pi times the radius squared multiplied by the height h.
The surface area is composed of two components. The area of the end - pi times the radius squared - multiplied by 3 because the tankage has two ends plus a wall between the two propellants plus the side of the tanks if you unrolled them which is the perimeter of the tank multiplied by the height, or 2 pi times the radius times the height.
We want to maximize the amount of volume and minimize the surface area to minimize the weight of the tank. There's an assumption there that the tank material is the same thickness throughout and I'm going to ignore the presence of any stiffeners in the tank.
How do the volume and surface area relate? What size tank would be the lightest for the volume that we need?

Rocket people often publish the mass of propellant for a stage, but they often do not publish the volume.
We can figure that out with some rocket math, and I'm going to walk you through it so that can make appropriate calculations when you are designing your next rocket.
We will start with our usual example, Falcon 9.
The Falcon 9 first stage carries - according to the figures I found - about 419,000 kilograms of propellant. It carries that in two separate tanks - one for the liquid oxygen and one for the RP-1 kerosene fuel. Those two propellants are different densities so we need to know how much of each we are carrying, and that's going to depend on the ratio of those two propellants that our engine burns.
That is known as the mixture ratio of the engine, and we can generally look it up. For the Merlin 1D engine, it's 2.36. Note that mixture ratios vary widely between different fuels because of the underlying chemistry.
What that number means is that for every 1 kilogram of fuel, the engine will consume 2.36 kilograms of liquid oxygen. That's a total of 3.36 kilograms of propellant, so we divide that 419,000 kilograms by 3.36 and get 125,000 kilograms of RP-1 and the remaining 294,000 kilograms is liquid oxygen.
We now know how much mass each tank holds but we want to know how much volume that takes up, so we will need to know the density of each propellant.
Liquid oxygen's density is easy to find - it's about 1141 kilograms per cubic meter. RP-1 presents a challenge - it's not one molecule but a mix of a whole bunch of different molecules so the density can vary - but I'm going to use 806 kilograms per cubic meter.
A simple division and we find out that we need 258 cubic meters to store the liquid oxygen and 155 cubic meters to store the RP-1.
That would be the right answer for most rockets, but SpaceX has to be different. They take advantage of the fact that if you chill the propellants, they get denser and you can therefore stuff more mass into the same space.
This works pretty well for liquid oxygen and you can get about 10% more density, up to about 1255 kilograms per cubic meter. RP-1 is less chillable as if you cool it too much it turns to gel, so we only get about 2% more density, up to 822 kilograms per cubic meter.
Redo the math, and we get 234 cubic meters for the liquid oxygen and 152 cubic meters for the RP-1. It's about 6.5% savings in volume.
Here's a summary of the improvements you can get through subchilling. The liquid hydrogen one looks useful but liquid hydrogen is so cold it's a huge effort to just keep it liquid so I'm not sure if subchilling would be practical.
Anyway, we now have a way to estimate how big the propellant tanks need to be for any rocket stage.
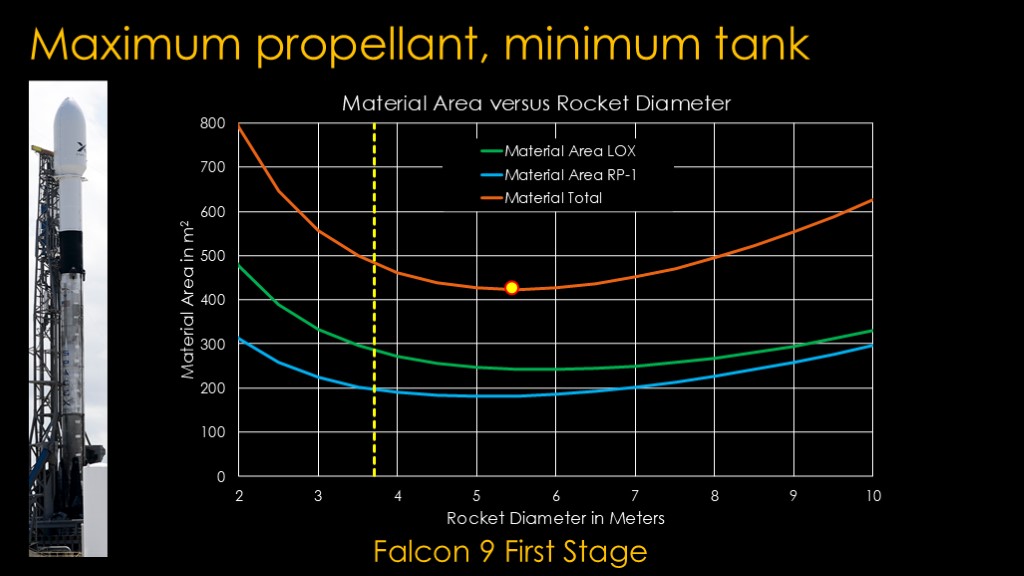
Now we can calculate how much material it will take to hold the propellant for a specific stage.
Excel coughed up this chart, starting with a very thin 2 meter rocket on the left and a fat 10 meter rocket on the right.
We can see that the total material required is at a minimum at around 5 meters in diameter.
The actual Falcon 9 is 3.7 meters in diameter, which means that the tanks uses about 13% more material than a 5 meter one would.
The obvious question at this point is "why isn't Falcon 9 a 5 meter rocket?"
The usual explanation is that it's because of the US road system.

Falcon 9 stages are made in Hawthorne California and need to be shipped either to nearby Vandenberg air force base or all the way across the country to Florida, and you can't practically truck rockets bigger than 3.7 meters.
5 meter rockets are generally shipped by ship.
So SpaceX accepted a slightly heavier rocket so that they could make transporting them much simpler.
That's the story why Falcon 9 is so tall and thin, but there's a little more nuance than that.
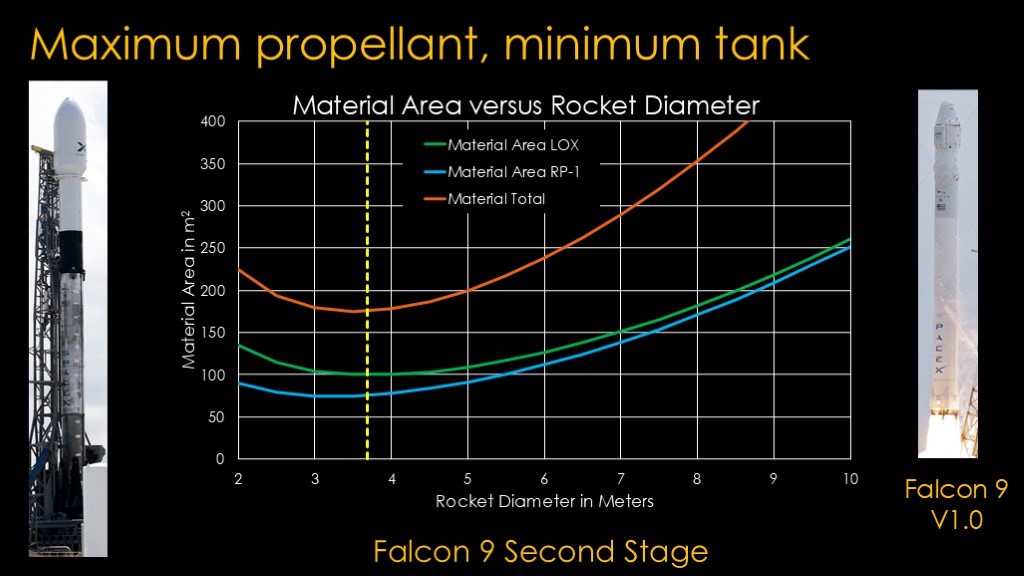
This is the same chart for the second stage tanks. Note that the minimum area is pretty much exactly at the 3.7 meter stage diameter.
So the SpaceX Falcon 9 has a second stage designed to be as light as possible - and therefore as performant as possible - and the first stage is then sized to be capable of doing what it needs to do to put the second stage in the right location. Efficiency is much more important for the second stage.
Interestingly, if you look at Falcon 9 version 1.0, you'll find that the second stage carried only about half the propellant of the V1.1 version. A 3 meter rocket would be better for performance for the V1.0 version. That suggests that the V1.1 size was what SpaceX had planned all along and just needed to wait for a higher thrust version of the Merlin engine to start flying it.
My usual explanation for Falcon 9 using an weird propellant combination for a second stage - RP-1 kerosene and liquid oxygen rather than the far more common liquid hydrogen and liquid oxygen - has been that it was easiest and quickest for them to adapt the merlin engine to be a vacuum engine, but this shows another reason - you can build a nice beefy second stage for a 3.7 meter rocket if you use RP-1 as the fuel.
Because SpaceX chose a small diameter rocket, using RP-1 for both stages was an excellent choice. If they had chosen to use hydrogen, the stages would have been optimal at 5 meters in diameter and therefore poor performers at 3.7 meters.
Speaking of hydrogen, let's look at the Vulcan rocket from ULA.
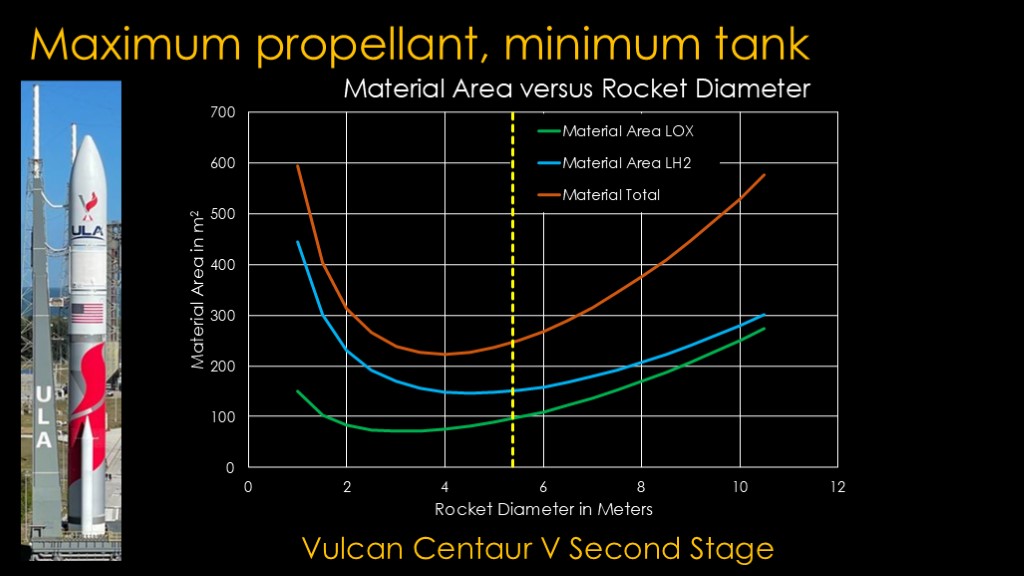
Here's the second stage for Vulcan. It's 5.4 meters in diameter, so it's about 10% bigger than the optimal size.
Its optimal size is actually pretty close to the Falcon 9 diameter, but because Centaur burns hydrogen, the centaur tanks are 50% bigger than the Falcon 9 ones but only hold half the propellant by mass.
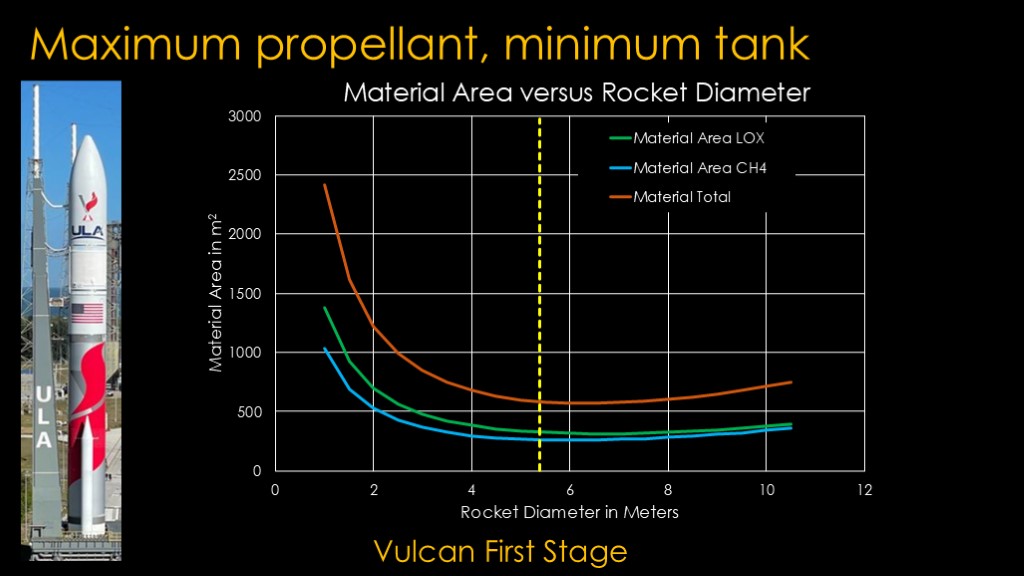
If we look at the first stage - which burns liquid methane and liquid oxygen - the diameter of Vulcan is pretty much the optimal size.
With Vulcan, 5.4 meters is great for the first stage but a little big for the second stage. My guess is that they made that choice because they wanted the very large 5.4 meter fairing size, and to put that on top of a small second stage on top of a big first stage would cost more in mass than just making centaur a little bit wider than it would like to be. Vulcan also stages much later than Falcon 9 so the first stage does more of the work and the second stage is less important.
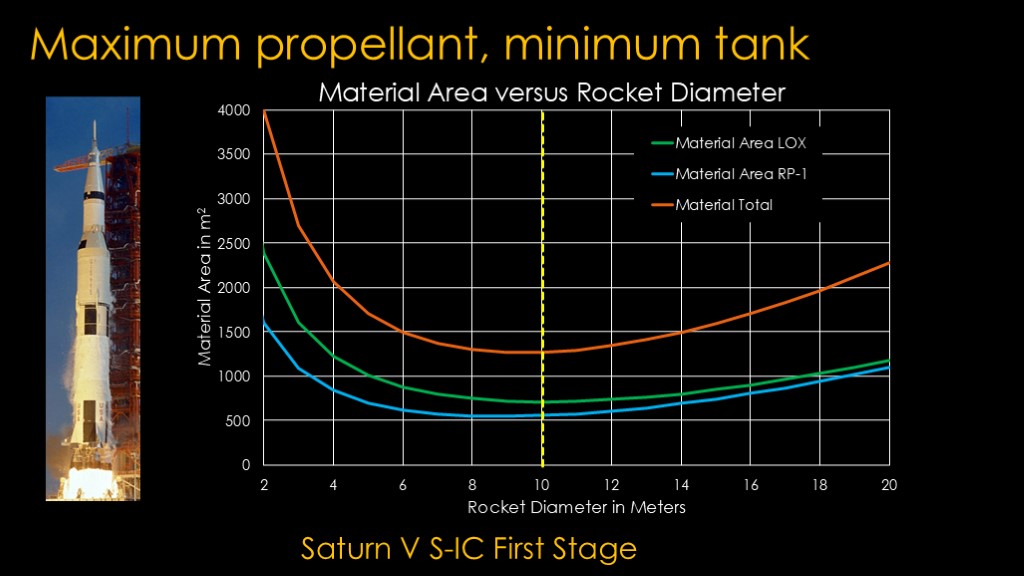
But what would you do if you had a case where you needed to have efficient sizes for 3 stages?
Like, say, you were building a moon rocket.
The first stage burns RP-1 kerosene and liquid oxygen, and the minimum material for the tank is pretty much exactly at the 10 meter size of the stage.
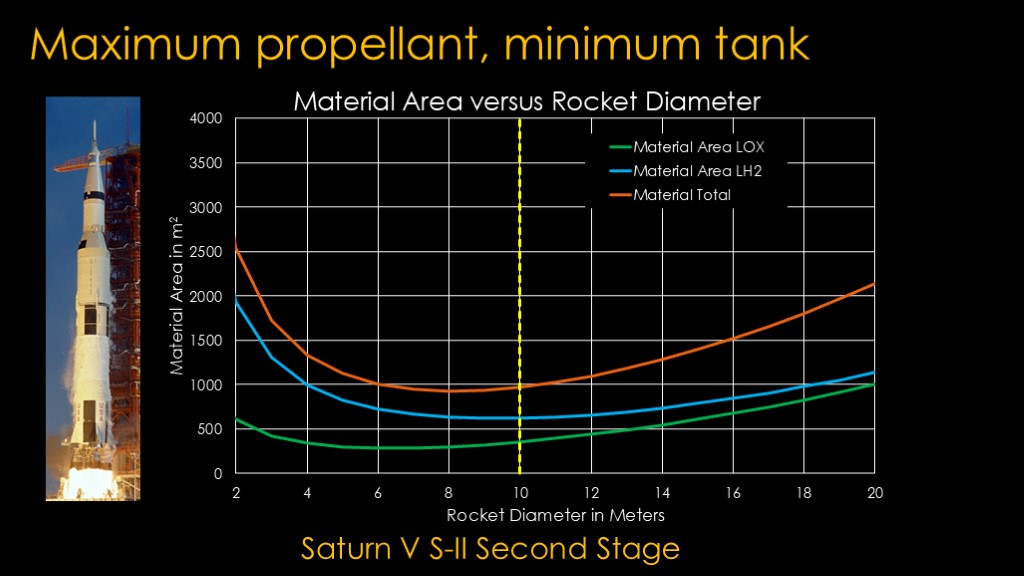
The second stage switches over to liquid hydrogen as the fuel, which naturally means that it is going to need more space for the fuel and a largish diameter.
The second stage stays at the 10 meter diameter - it could have worked a tiny bit better at 8 meters but the difference is small and 10 meters makes the overall rocket a little shorter.
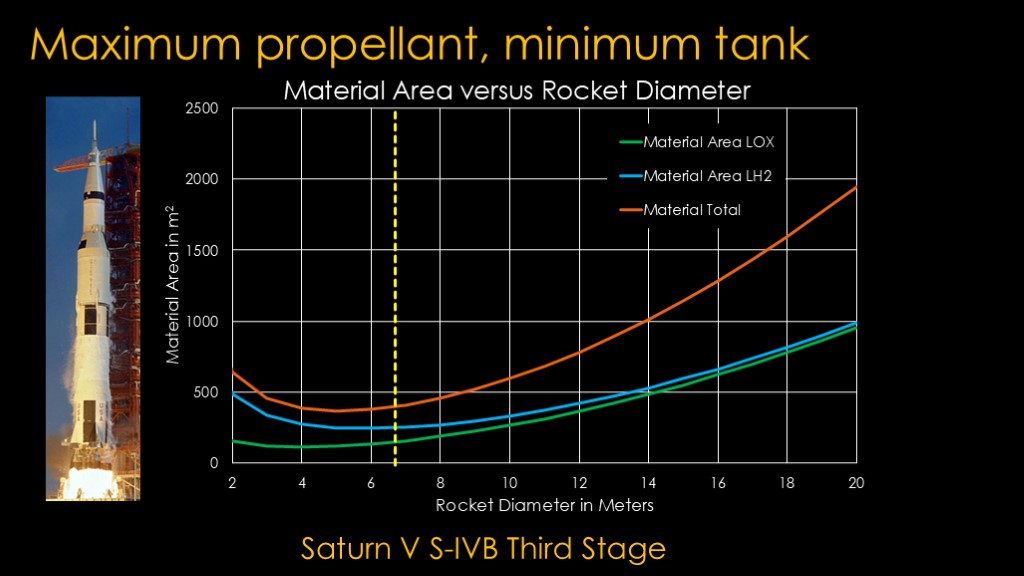
The third stage also uses liquid hydrogen but carries less propellant.
It not surprisingly prefers a smaller diameter of about 5 meters, but it's pretty good at the actual 6.8 meter diameter. If it had maintained the 10 meter diameter, it would use 50% more material in its tanks than it did at 6.8 meters
The third stage really needs to be light and efficient, so the tank size choice needs to be close to optimal.
And that explains why the Saturn V has that weird step between the second and third stages.

Wasn't this talk about bigger starships?
Well, yes, but I needed to cover how tank sizing works I got carried away because it's an interesting topic.
We'll start with the same chart for starship
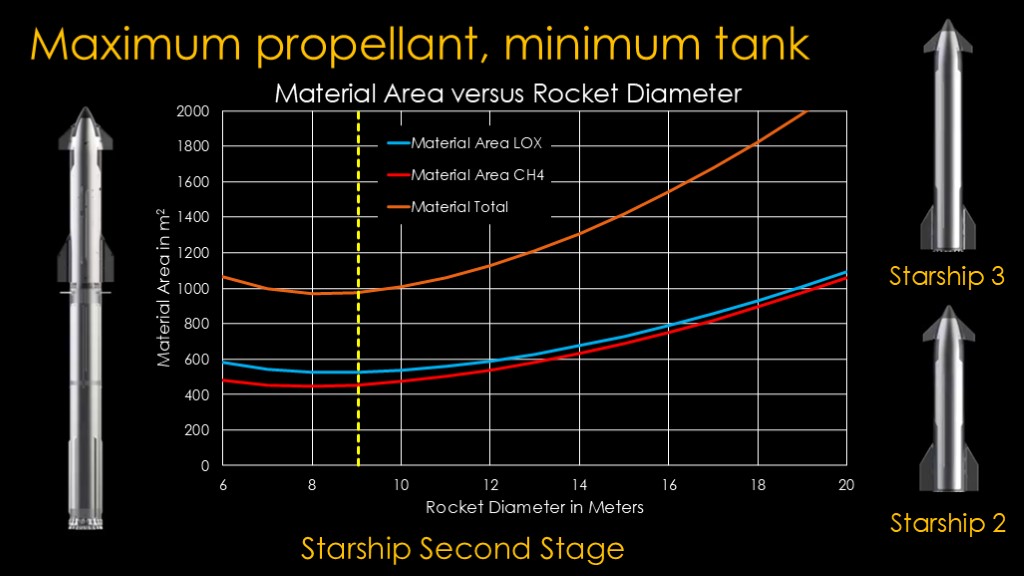
This is the Starship 1 variant that flew in IFT1-4.
The 9 meter tank is a little big, but it's a small difference.
I don't show the newly proposed versions on the chart.
The Starship 2 version carries just a little more fuel and is pretty much perfect.
The Starship 3 version would prefer to be 10 meters in diameter, but it's only a 2% difference in tank area.
This suggests that SpaceX had the Starship 2 version in mind but needed to make sure they had enough engine thrust to make it work. Sounds similar to Falcon 9.
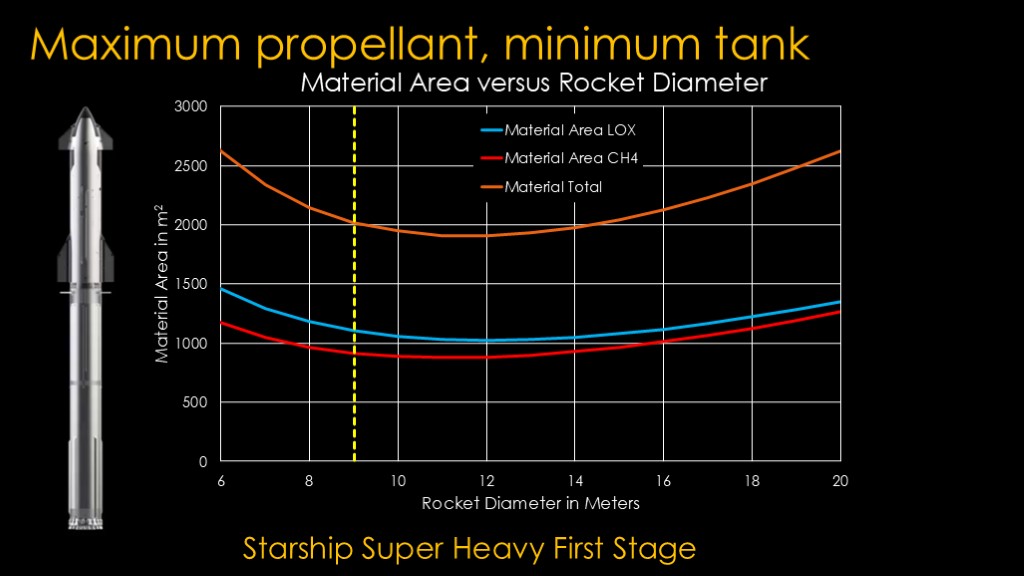
For the super heavy first stage, it's the same story as the Falcon 9 first stage; it's smaller than optimum so that the second stage can be close to optimum. The best size would be about 11 meters.
The starship 2 and 3 versions would be happier at 12 meters, but they stay at 9 meters.

Back to the original topic, which is whether physics prefers rockets of unusual size and therefore would a larger starship be better?
Or, to put it another way, how do our calculations change as the diameter gets bigger.
I've rearranged the equations a bit so that that things are a bit clearer.
If we look at these two terms, both have pi times r squared in them, but the volume is h times that and the surface area is only 3 times that, so if h is more than 3, increases in the radius will cause the volume to increase faster than the surface area.
If we look at these two terms we can see that the first one uses radius squared while the second one uses the radius, so the once again the volume will increase faster.
But what if you put the two surface area terms together?
There are mathematical ways to answer that question - you calculus folks can figure it out - but I prefer a good graph.
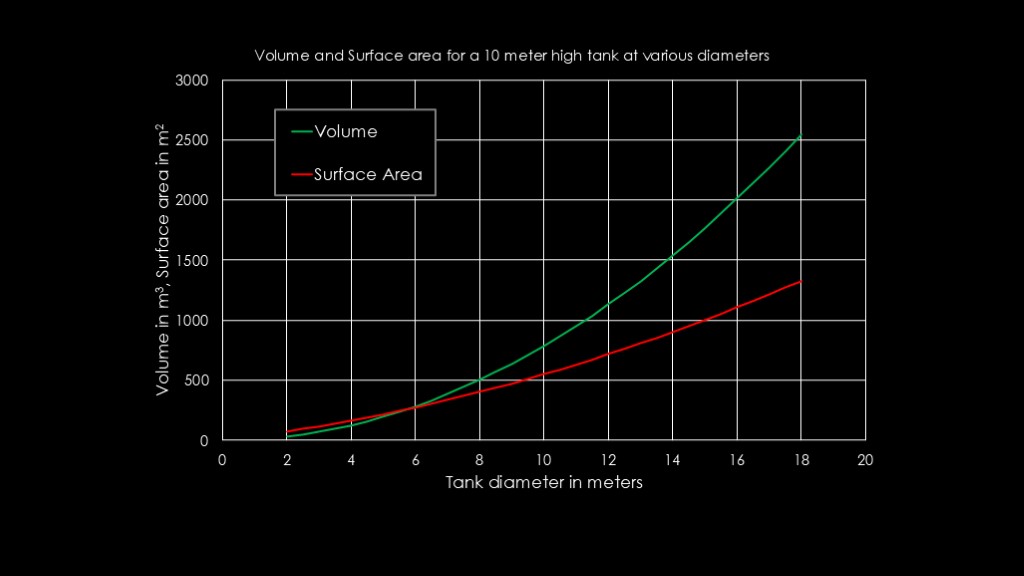
If we arbitrarily choose a 10 meter high tank, we see that the volume increases faster than the surface area, which means that bigger tank diameters are better and therefore bigger rockets are better.
But it's not quite that simple...
We know that the optimal diameter depends on how much propellant we want to carry, so we want a different graph that is specific to starship
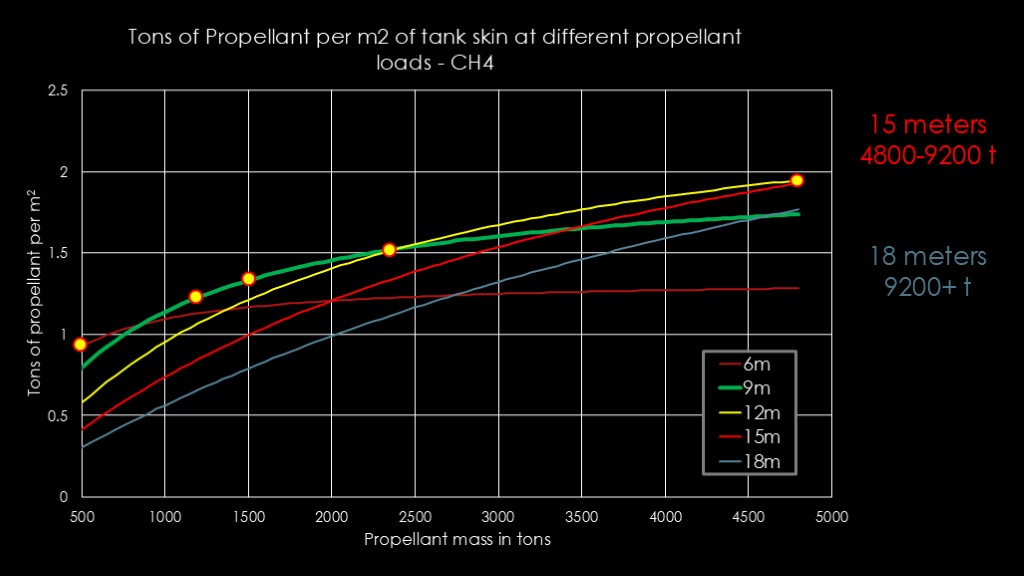
This is a graph that shows us how many tons we can put into a tank per square meter of tank skin at different propellant amounts for a rocket burning liquid methane. And this is aimed at Starship, not at Super Heavy, because this measure is far more important for Starship.
We see two things.
The first is that you do need to choose your rocket diameter based on the amount of propellant you want. If you are only carrying 500 tons, you get far better performance from a 6 meter rocket than the larger sizes.
The 9 meter diameter is not surprisingly the best choice for 1200 tons of propellant carried by the current starship. It's also the best choice for the 1500 tons that starship 2 will carry. Interestingly, the 2300 tons that Starship 3 is currently projected to carry is right at the transition point where a 9 meter and 12 meter size are roughly equal. You can still get gains at 9 meters and larger propellant amounts but you would do better with a bigger rocket.
The other thing to notice is that as you increase propellant, a large diameter becomes a better choice at a specific propellant range. I'm a bit surprised to find that 12 meters is still the best choice even if you go up to 4800 tons of propellant, which is 4 times what starship currently carries. That is a much bigger rocket.
And because I know somebody is going to ask, 15 meters reigns from 4800 to 9200 tons, and then 18 meters takes over
And of course there are intermediate curves for diameters between the ones I list, but 5 lines on a chart is already too many.
It is, of course, more complicated than that.
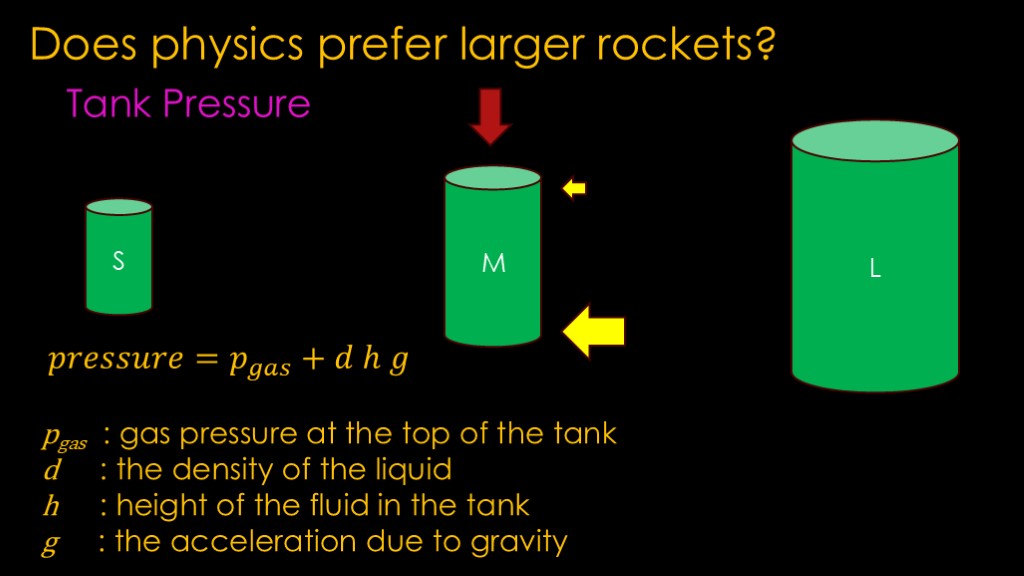
We also need to talk about tank pressure.
In pressure tank design, tank wall thickness goes up as tank size increases, so the gain that you see in terms of more propellant per square meter may not help if you need to increase your tank wall thickness.
The question is whether thinking of them as pressure tanks is the right thing to do. Liquid propellant ullage tank pressure - the pressure above the propellant - is fairly low for pump-fed engines - somewhere from maybe 15 to 60 psi, or only 1-4 bar. That's not a lot, and these tanks have to carry significant loads through their sides when the rocket is operating, and those loads likely set the tank thickness more than the pressure.
And just to make it more confusing, the pressure at the top of the tank is just the gas pressure but the pressure at the bottom of the tank is dependent on how tall the tank is the density of the propellant. The pressure is equal to the pressure of the gas at the top of the tank plus the density of the liquid multiplied by the height of the fluid in the tank multiplied by the acceleration due to gravity. That means there is higher pressure at the bottom of the tank and on the sides right next to the bottom than at the top.
And to add another factor, the acceleration due to gravity goes up during the flight of the stage which will increase the pressure on the tank but the height of fluid in the tank goes down during the flight which will reduce the pressure, and that will complicate the calculation of the maximum pressure in the tank.
It's complex, but since the engineers seem to believe that bigger diameter is still better from an engineering perspective, I'm going to go with them.

There are, of course, other considerations...
That huge factory that SpaceX built at Boca Chica is sized to deal with 9 meter rockets, both from a diameter standpoint and from a height standpoint. The buildings would have to be expanded to deal with a bigger rocket.
It's no surprise that super heavy doesn't get much longer because there's not much room left in the high bays for a taller stage.

Starship and super heavy are transported on these large self propelled transporters from Roll Lift. Even at 9 meters, they require the whole width of the road plus the shoulders. Bigger means bigger infrastructure.

And everything at the launch pad needs to get bigger.
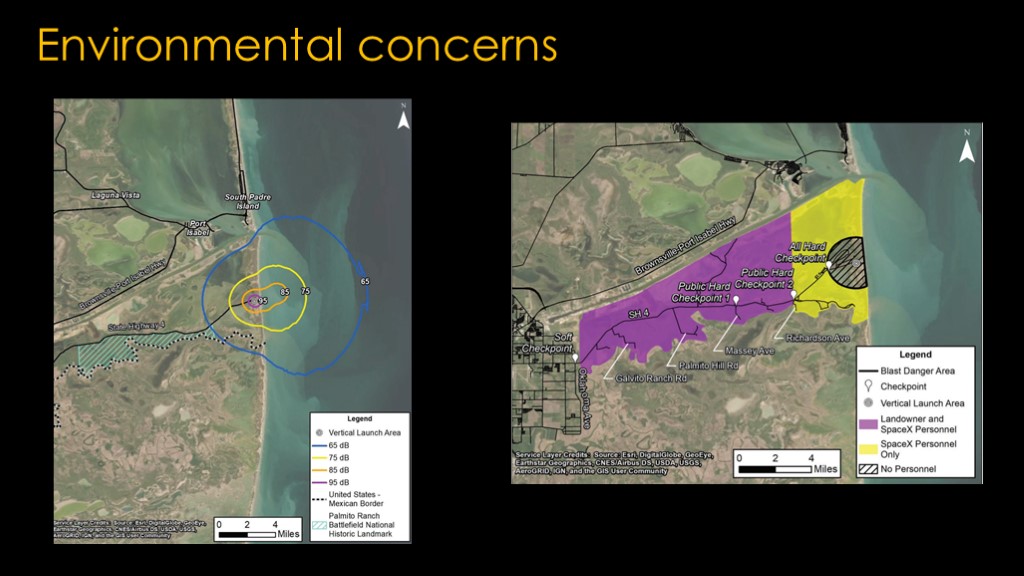
There are also environmental concerns. A bigger rocket means higher peak sound levels at both Boca Chica and Kennedy, and it also mean a larger blast damage footprint and larger "keep out" zones.

It's not clear what kind of vehicle Starship is at this point.
Is it a regional jet like the bombardier CRJ700 that is used primarily on short routes.
Is it like the 737 or Airbus' A320, the absolute workhorses of the industry.
Or is it like Airbus' A380, a plane that ended up too big for the market.
At this point we don't know. If starship is the 737, maybe it doesn't get any bigger.

We therefore end up with a big question mark. There are some advantages to bigger vehicles but there are also some significant costs and other issues that would come with a larger diameter.
My guess is that they will likely stick with the 9 meter diameter for the near future - say the next 5 years - until they really understand the system well. After that, I don't have a real opinion. Build hundreds or even thousands of the 9 meter variant so that they are cheap, or upgrade to a 12 or 15 meter vehicle so they are individually a lot more capable.
We'll just have to wait and see...
If you enjoyed this video, please send me this poster....